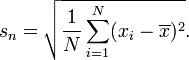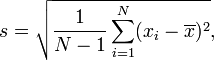Почему школы США и Великобритании обучают различным методам расчета стандартного отклонения?

Как я понимаю, в школах Великобритании учат, что стандартное отклонение определяется с использованием:

в то время как школы США преподают:

(на базовом уровне в любом случае).

В прошлом это вызывало проблемы у моих студентов, которые искали в Интернете, но нашли неверное объяснение.

Почему разница?

С простыми наборами данных, скажем, 10 значений, какая будет ошибка, если будет применен неправильный метод (например, на экзамене)?

Первая формула представляет собой стандартное отклонение совокупности, а вторая формула представляет собой стандартное отклонение выборки . Вторая формула также связана с непредвзятой оценкой дисперсии - подробности см. В Википедии .

Я полагаю (здесь) в Великобритании, они не делают различий между выборкой и населением в старшей школе. Они, конечно, не касаются таких понятий, как необъективные оценки.

Поскольку еще никто не ответил на последний вопрос - а именно, чтобы количественно оценить различия между двумя формулами - давайте позаботимся об этом.

По многим причинам целесообразно сравнивать стандартные отклонения с точки зрения их соотношений, а не их различий. Соотношение

Аппроксимацию можно рассматривать как усечение (чередующихся) рядов Тейлора для квадратного корня, указывая на то, что ошибка не может превышать =1/(8N2). Это устанавливает, что приближение более чем достаточно (для наших целей) один раз$|\binom{1/2}{2}N^{-2}|$$1 / (8 N^2)$ равно 2 или больше.$N$$2$

Очевидно, что две оценки SD находятся в пределах (примерно) 10% друг от друга, как только превышает 5 , и в пределах 5%, когда N превышает$N$$5$$N$ , и так далее. Очевидно, что для многих целей эти расхождения настолько малы, что не имеет значения, какая формула используется, особенно когда SD предназначен дляописанияраспространения данных или дляполуколичественныхоценок или прогнозов (например, при использовании 68-95 -99,7 эмпирическое правило). Расхождения еще менее важны присравнении$10$SD, например, при сравнении спредов двух наборов данных. (Когда наборы данных равносильны, расхождения фактически полностью исчезают, и обе формулы приводят к одинаковым выводам.) Возможно, это те формы рассуждений, которые мы пытаемся преподавать начинающим ученикам, поэтому, если ученики начинают интересоваться, какую формулу использовать, это может быть воспринято как знак того, что текст или класс не в состоянии подчеркнуть то, что действительно важно.

$N$$t$$z$$s$$s_n$

Это исправление Бесселя . Версия для США показывает формулу для стандартного отклонения выборки , где версия для Великобритании выше является стандартным отклонением выборки .

Я не уверен, что это чисто американский или британский вопрос. Остальная часть этой страницы взята из FAQ, который я написал ( http://www.graphpad.com/faq/viewfaq.cfm?faq=1383 ).

Как вычислить SD с n-1 в знаменателе

1. Вычислите квадрат разности между каждым значением и значением выборки.

2. Добавьте эти значения вверх.

3. Разделите сумму на n-1. Результат называется дисперсией.

4. Возьмите квадратный корень, чтобы получить стандартное отклонение.

Почему н-1?

Зачем делить на n-1, а не n при вычислении стандартного отклонения? На шаге 1 вы вычисляете разницу между каждым значением и средним значением этих значений. Вы не знаете истинного среднего значения населения; все, что вы знаете, это среднее значение вашего образца. За исключением редких случаев, когда среднее значение выборки оказывается равным среднему значению для популяции, данные будут ближе к среднему значению для выборки, чем к истинному среднему значению для популяции. Таким образом, значение, которое вы вычисляете на шаге 2, вероятно, будет немного меньше (и не может быть больше), чем это было бы, если бы вы использовали истинное среднее значение на шаге 1. Чтобы восполнить это, разделите на n-1, а чем Н.В. Это называется коррекция Бесселя.

Но почему н-1? Если вы знали среднее значение выборки и все значения, кроме одного, вы могли бы рассчитать, каким должно быть это последнее значение. Статистики говорят, что существует n-1 степеней свободы.

Когда следует вычислять SD с помощью знаменателя n вместо n-1?

В статистических книгах часто приводятся два уравнения для вычисления SD: одно с использованием n, а другое с использованием n-1 в знаменателе. Некоторые калькуляторы имеют две кнопки.

Уравнение n-1 используется в общей ситуации, когда вы анализируете выборку данных и хотите сделать более общие выводы. SD, рассчитанная таким образом (с n-1 в знаменателе), является вашей лучшей оценкой значения SD в общей популяции.

Если вы просто хотите количественно оценить вариацию в конкретном наборе данных и не планируете экстраполировать, чтобы сделать более широкие выводы, то вы можете вычислить SD, используя n в знаменателе. В результате SD является SD этих конкретных значений. Нет смысла вычислять SD таким образом, если вы хотите оценить SD населения, из которого были получены эти точки. Использовать n в знаменателе имеет смысл только тогда, когда нет выборки из совокупности, нет желания делать общие выводы.

Цель науки - почти всегда обобщать, поэтому не следует использовать уравнение с n в знаменателе. Единственный пример, который я могу придумать, где это может иметь смысл, - это количественная оценка различий между результатами экзаменов. Но гораздо лучше было бы показать диаграмму рассеяния каждой оценки или гистограмму распределения частот.

Поскольку N - это число точек в наборе данных, можно утверждать, что, вычисляя среднее значение, можно уменьшить степень свободы в наборе данных на единицу (поскольку каждый вводил зависимость в набор данных), поэтому следует использовать N -1 при оценке стандартного отклонения от набора данных, для которого нужно было предварительно оценить среднее значение.