Предполагая, что переменные положительные или неотрицательные, ребра ребра - это просто точки, за которыми данные станут 0 или отрицательными соответственно. Поскольку такие реальные данные имеют тенденцию к правильному искажению, мы видим большую плотность точек на нижнем конце их распределения и, следовательно, большую плотность в «точке» клина.
В более общем смысле, PCA - это просто ротация данных, и ограничения на эти данные, как правило, будут видны в основных компонентах так же, как показано в вопросе.
Вот пример использования нескольких нормально распределенных переменных:
library("vegan")
set.seed(1)
df <- data.frame(matrix(rlnorm(5*10000), ncol = 5))
plot(rda(df), display = "sites")

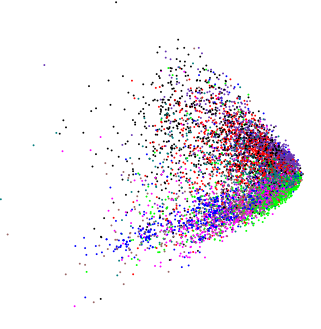
В зависимости от поворота, подразумеваемого первыми двумя ПК, вы можете увидеть клин или несколько другую версию, показанную здесь в 3d с использованием ( ordirgl()вместо plot())

Здесь в 3d мы видим несколько шипов, выступающих из центральной массы.
Икся∼ ( N) ( μ = 0 , σ= 1 )
set.seed(1)
df2 <- data.frame(matrix(rnorm(5*10000), ncol = 5))
plot(rda(df2), display = "sites")


А для равномерных положительных случайных величин мы видим куб
set.seed(1)
df3 <- data.frame(matrix(runif(3*10000), ncol = 3))
plot(rda(df3), display = "sites")


Обратите внимание, что здесь для иллюстрации я показываю форму, используя всего 3 случайные величины, поэтому точки описывают куб в 3d. При более высоких измерениях / большем количестве переменных мы не можем идеально представить 5-мерный гиперкуб в 3d, и, следовательно, отчетливая форма "куба" несколько искажается. Подобные проблемы влияют на другие показанные примеры, но все еще легко увидеть ограничения в этих примерах.
Для ваших данных лог-преобразование переменных до PCA вытягивало бы хвосты и растягивало сгруппированные данные так же, как вы могли бы использовать такое преобразование в линейной регрессии.
Другие формы могут возникать на участках PCA; одна такая форма представляет собой артефакт метрического представления, сохраняемый в PCA и известный как подкова . Для данных с длинным или доминирующим градиентом (хорошо известно, что выборки, расположенные вдоль одного измерения с переменными, увеличивающимися от 0 до максимума, а затем снова уменьшающимися до 0 по частям данных, генерируют такие артефакты. Рассмотрим
ll <- data.frame(Species1 = c(1,2,4,7,8,7,4,2,1,rep(0,10)),
Species2 = c(rep(0, 5),1,2,4,7,8,7,4,2,1, rep(0, 5)),
Species3 = c(rep(0, 10),1,2,4,7,8,7,4,2,1))
rownames(ll) <- paste0("site", seq_len(NROW(ll)))
matplot(ll, type = "o", col = 1:3, pch = 21:23, bg = 1:3,
ylab = "Abundance", xlab = "Sites")

которая производит крайнюю подкову, где точки на концах осей изгибаются обратно в середину.

 .
. (за исключением этого случая, я действительно хотел узнать, существует ли какая-либо внутренняя структура).
(за исключением этого случая, я действительно хотел узнать, существует ли какая-либо внутренняя структура).






