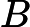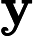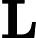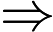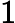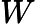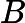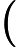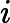Почему Python scikait-learn LDA не работает правильно и как он вычисляет LDA через SVD?

Я использовал Линейный Дискриминантный Анализ (LDA) из scikit-learnбиблиотеки машинного обучения (Python) для уменьшения размерности, и мне было немного интересно узнать о результатах. Теперь мне интересно, что scikit-learnделает LDA , чтобы результаты выглядели иначе, чем, например, ручной подход или LDA, выполненные в R. Было бы здорово, если бы кто-то мог дать мне некоторое представление здесь.

Что в основном больше всего беспокоит то, что scikit-plotпоказывает корреляцию между двумя переменными, где должна быть корреляция 0.

Для теста я использовал набор данных Iris, и первые 2 линейных дискриминанта выглядели так:

IMG-1. LDA через scikit-Learn

введите описание изображения здесь

Это в основном согласуется с результатами, которые я нашел в документации scikit-learn здесь.

Теперь, я прошел через LDA шаг за шагом и получил другой прогноз. Я попробовал разные подходы, чтобы выяснить, что происходит:

IMG-2. LDA на необработанных данных (без центрирования, без стандартизации)

введите описание изображения здесь

И здесь был бы пошаговый подход, если бы я сначала стандартизировал (нормализация по z-шкале; дисперсия единиц). Я сделал то же самое только со средним центрированием, что должно привести к тому же относительному проекционному изображению (и это действительно так).

IMG-3. Пошаговое LDA после центрирования или стандартизации

введите описание изображения здесь

IMG-4. LDA в R (настройки по умолчанию)

LDA в IMG-3, где я центрировал данные (что было бы предпочтительным подходом), выглядит также точно так же, как тот, который я нашел в Посте кем-то, кто делал LDA в R введите описание изображения здесь

Код для справки

Я не хотел вставлять здесь весь код, но я загрузил его как записную книжку IPython, разбитую на несколько шагов, которые я использовал (см. Ниже) для проекции LDA.

Шаг 1: Вычисление d-мерных средних векторов $m_{i} = \frac{1}{n_{i}} \sum_{x \in D_{i}}^{n} x_{k}$ $\mathbf m_i = \frac{1}{n_i} \sum\limits_{\mathbf x \in D_i}^n \; \mathbf x_k$
Шаг 2: Вычисление матриц рассеяния

2.1. Матрица рассеяния внутри класса вычисляется по следующему уравнению: $S_W$

$S_{W} = \sum_{i = 1}^{c} S_{i} = \sum_{i = 1}^{c} \sum_{x \in D_{i}}^{n} (x - m_{i}) (x - m_{i})^{T}$ $S_W = \sum\limits_{i=1}^{c} S_i = \sum\limits_{i=1}^{c} \sum\limits_{\mathbf x \in D_i}^n (\mathbf x - \mathbf m_i)\;(\mathbf x - \mathbf m_i)^T$
2.2 Матрица рассеяния между классами вычисляется по следующему уравнению: где - общее среднее. $S_B$

$S_{B} = \sum_{i = 1}^{c} n_{i} (m_{i} - m) (m_{i} - m)^{T}$ $S_B = \sum\limits_{i=1}^{c} n_i (\mathbf m_i - \mathbf m) (\mathbf m_i - \mathbf m)^T$ $\mathbf m$
Шаг 3. Решение обобщенной задачи на собственные значения для матрицы $S_{W}^{-1}S_B$

3.1. Сортировка собственных векторов по убыванию собственных значений

3.2. Выбор k собственных векторов с наибольшим собственным значением. Объединение двух собственных векторов с наивысшими собственными значениями для построения нашей -мерной матрицы собственных векторов $d \times k$ $\mathbf W$
Шаг 5: Преобразование выборок в новое подпространство
$y = W^{T} \times x .$ $\mathbf y = \mathbf W^T \times \mathbf x.$

— амеба говорит восстановить монику
источник

Я не изучал различия, но вы можете точно увидеть, что делает scikit-learn в исходном коде .

— Дугал

Похоже, что они также стандартизируют (центрируют, а затем масштабируют посредством деления на стандартное отклонение). Это, я ожидал бы результат, подобный тому в моем 3-м графике (и R) заговор ... хмм

Странно: сюжет, который вы получили с помощью scikit (и того, что они показывают в своей документации), не имеет смысла. LDA всегда дает проекции, которые имеют нулевую корреляцию, но, очевидно, существует очень сильная корреляция между проекциями скикита на дискриминантных осях 1 и 2. Там что-то явно не так.

— говорит амеба: восстановите Монику

@ameoba Да, я тоже так думаю. Также странно то, что тот же график, который я показываю для scikit, приведен в документации к примеру: scikit-learn.org/stable/auto_examples/decomposition/… Это заставляет меня думать, что мое использование scikit правильное, но есть что-то странное о функции LDA

@SebastianRaschka: Да, я заметил. Это действительно странно. Тем не менее, обратите внимание, что первый из ваших собственных (не скикитных) графиков LDA также показывает ненулевую корреляцию, и, следовательно, что-то должно быть не так с ним. Вы центрировали данные? Проекция на вторую ось, похоже, не имеет нулевого среднего.

— говорит амеба: восстановите Монику

Ответы:

Обновление: благодаря этому обсуждению scikit-learnбыл обновлен и теперь работает правильно. Его исходный код LDA можно найти здесь . Первоначальная проблема возникла из-за незначительной ошибки (см. Это обсуждение на github ), и мой ответ на самом деле не указывал на нее правильно (извинения за возникшую путаницу). Поскольку все это больше не имеет значения (ошибка исправлена), я отредактировал свой ответ, чтобы сосредоточиться на том, как LDA может быть решено с помощью SVD, который является алгоритмом по умолчанию в scikit-learn.

После определения матриц рассеяния внутри и между классами и стандартный расчет LDA, как указано в вашем вопросе, состоит в том, чтобы взять собственные векторы в качестве дискриминантных осей ( см., например, здесь ). Однако те же оси можно вычислить немного по-другому, используя отбеливающую матрицу: $\boldsymbol \Sigma_W$ $\boldsymbol \Sigma_B$ $\boldsymbol \Sigma_W^{-1} \boldsymbol \Sigma_B$

Вычислить . Это отбеливающая трансформация по отношению к объединенной ковариации внутри класса (подробности см. В моем связанном ответе). $\boldsymbol \Sigma_W^{-1/2}$

Обратите внимание, что если у вас есть собственное разложение , то . Также обратите внимание, что можно вычислить то же самое, выполнив SVD для объединенных данных класса: . $\boldsymbol \Sigma_W = \mathbf{U}\mathbf{S}\mathbf{U}^\top$ $\boldsymbol \Sigma_W^{-1/2}=\mathbf{U}\mathbf{S}^{-1/2}\mathbf{U}^\top$ $\mathbf{X}_W = \mathbf{U} \mathbf{L} \mathbf{V}^\top \Rightarrow \boldsymbol\Sigma_W^{-1/2}=\mathbf{U}\mathbf{L}^{-1}\mathbf{U}^\top$
Найдите собственные векторы , назовем их . $\boldsymbol \Sigma_W^{-1/2} \boldsymbol \Sigma_B \boldsymbol \Sigma_W^{-1/2}$ $\mathbf{A}^*$

Опять же, обратите внимание, что его можно вычислить, выполнив SVD данных между классами , преобразованных с помощью , то есть данных между классами, отбеленных по отношению к классу внутри класса. ковариации. $\mathbf{X}_B$ $\boldsymbol \Sigma_W^{-1/2}$
Оси дискриминанта будут заданы как , то есть главными осями преобразованных данных, преобразованных снова . $\mathbf A$ $\boldsymbol \Sigma_W^{-1/2} \mathbf{A}^*$

Действительно, если является собственным вектором указанной матрицы, то и умножение слева на и определение , мы сразу получаем : $\mathbf a^*$
$Σ_{W}^{- 1 / 2} Σ_{B} Σ_{W}^{- 1 / 2} a^{*} = λ a^{*},$ $\boldsymbol \Sigma_W^{-1/2} \boldsymbol \Sigma_B \boldsymbol \Sigma_W^{-1/2}\mathbf a^* = \lambda \mathbf a^*,$ $\boldsymbol \Sigma_W^{-1/2}$ $\mathbf a = \boldsymbol \Sigma_W^{-1/2}\mathbf a^*$ $Σ_{W}^{- 1} Σ_{B} a = λ a .$ $\boldsymbol \Sigma_W^{-1} \boldsymbol \Sigma_B \mathbf a = \lambda \mathbf a.$

Таким образом, LDA эквивалентно отбеливанию матрицы средних классов в отношении ковариации внутри класса, выполнению PCA на средних классах и обратному преобразованию результирующих главных осей в исходное (неотбеленное) пространство.

На это указывает, например, «Элементы статистического обучения» , раздел 4.3.3. В scikit-learnэто путь по умолчанию для вычисления LDA , потому что SVD матрицы данных численно более стабильны , чем о собственных разложении его ковариационной матрицы.

Обратите внимание, что вместо можно использовать любое отбеливающее преобразование, и все будет работать точно так же. В (вместо ) и это работает просто отлично (вопреки тому, что изначально было написано в моем ответе). $\boldsymbol \Sigma_W^{-1/2}$ scikit-learn $\mathbf{L}^{-1}\mathbf{U}^\top$ $\mathbf{U}\mathbf{L}^{-1}\mathbf{U}^\top$

— амеба говорит восстановить монику
источник

Спасибо за этот хороший ответ. Я ценю то, что вы нашли время, чтобы написать это так красиво. Может быть, вы могли бы упомянуть об этом в обсуждении на GitHub; Я уверен, что это поможет исправить LDA в следующей версии sci-kit

@SebastianRaschka: У меня нет аккаунта на GitHub. Но если вы хотите, вы можете дать там ссылку на эту тему.

— говорит амеба, восстанови Монику

@amoeba: Учебники обычно описывают LDA так, как вы это делали - разложение по собственным значениям . Любопытно, что многие известные мне реализации LDA используют другой подход. Их оси - векторы к классу, преобразованному с помощью . Ваше решение LDA является ортонормированной основой этих векторов. LDA Scikit-learn дает те же результаты, что и эти реализации, поэтому я не думаю, что на самом деле есть ошибка.

Σ_{W}^{- 1} Σ_{B}

$\boldsymbol \Sigma_W^{-1} \boldsymbol \Sigma_B$

Σ_{W}^{- 1}

$\boldsymbol \Sigma_W^{-1}$

— Каземакасе

Для справки вот реализации, о которых я говорил: sourceforge.net/p/mlpy/code/ci/default/tree/mlpy/da.py#l24 github.com/sccn/BCILAB/blob/master/code/machine_learning /… Mathworks.com/matlabcentral/fileexchange/…

— kazemakase

@kazemakase: Ну, конечно, если есть только два класса, то имеет ранг 1, и все значительно упрощается, поскольку единственный собственный вектор задается как , где - классовые средства. Я думаю, это то, что вы имели в виду раньше? Это хорошо описано, например, в учебнике по епископу по ОД, раздел 4.1.4. Но обобщение на большее количество классов требует собственного анализа (там же, 4.1.6). Кроме того , код scikit ( в том , что мы обсуждаем здесь!) Делает использование СВД, два раза на самом деле.