Раздельные полигоны по пересечению с использованием PostGIS

У меня есть таблица полигонов PostGIS, где некоторые пересекаются друг с другом. Вот что я пытаюсь сделать:

• Для данного полигона, выбранного по id, дайте мне все полигоны, которые пересекаются. В основном,select the_geom from the_table where ST_Intersects(the_geom, (select the_geom from the_table where source_id = '123'))
• Из этих многоугольников мне нужно создать новые многоугольники, чтобы пересечение стало новым многоугольником. Поэтому, если многоугольник A пересекается с многоугольником B, я получу 3 новых многоугольника: A минус AB, AB и B минус AB.

Любые идеи?

Поскольку вы сказали, что получаете группу пересекающихся многоугольников для каждого интересующего вас многоугольника, вы можете создать так называемый «наложение многоугольника».

Это не совсем то, что делает решение Адама. Чтобы увидеть разницу, взгляните на эту картинку пересечения ABC:

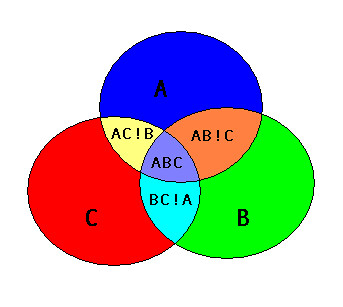
Я полагаю, что решение Адама создаст многоугольник "AB", который охватывает как области "AB! C" и "ABC", так и многоугольник "AC", который охватывает "AC! B" и "ABC", а также " До н.э. "многоугольник" это "BC! A" и "ABC". Таким образом, выходные полигоны "AB", "AC" и "BC" будут перекрывать область "ABC".

Наложение полигонов создает неперекрывающиеся полигоны, поэтому AB! C будет одним полигоном, а ABC будет одним полигоном.

Создание наложения полигонов в PostGIS на самом деле довольно просто.

Есть в основном три шага.

Шаг 1 - извлечение линии [обратите внимание, что я использую внешнее кольцо многоугольника, оно становится немного сложнее, если вы хотите правильно обрабатывать отверстия]:

SELECT ST_ExteriorRing(polygon_col) AS the_geom FROM my_table) AS lines

Шаг 2 состоит в том, чтобы "узить" линию (создать узел на каждом перекрестке). В некоторых библиотеках, таких как JTS, есть классы «Noder», которые вы можете использовать для этого, но в PostGIS функция ST_Union сделает это за вас:

SELECT ST_Union(the_geom) AS the_geom FROM (...your lines...) AS noded_lines

Шаг 3 - создать все возможные непересекающиеся многоугольники, которые могут приходить из всех этих линий, что делается функцией ST_Polygonize :

SELECT ST_Polygonize(the_geom) AS the_geom FROM (...your noded lines...)

Вы можете сохранить выходные данные каждого из этих шагов во временную таблицу или объединить их все в один оператор:

CREATE TABLE my_poly_overlay AS
SELECT geom FROM ST_Dump((
    SELECT ST_Polygonize(the_geom) AS the_geom FROM (
        SELECT ST_Union(the_geom) AS the_geom FROM (
            SELECT ST_ExteriorRing(polygon_col) AS the_geom FROM my_table) AS lines
        ) AS noded_lines
    )
)

Я использую ST_Dump, потому что выходные данные ST_Polygonize являются коллекцией геометрии, и (обычно) удобнее иметь таблицу, в которой каждая строка является одним из полигонов, составляющих наложение полигонов.

Если я правильно понимаю, Вы хотите взять (A - левая геометрия, B - правая):

Изображение A∪B http://img838.imageshack.us/img838/3996/intersectab1.png

И извлечь:

∖ AB

Изображение A ∖ AB http://img830.imageshack.us/img830/273/intersectab2.png

AB

Изображение AB http://img828.imageshack.us/img828/7413/intersectab3.png

и B ∖ AB

Изображение B ∖ AB http://img839.imageshack.us/img839/5458/intersectab4.png

То есть - три разные геометрии для каждой пересекающейся пары.

Сначала давайте создадим вид всех пересекающихся геометрий. Предполагая, что ваша таблица называется polygons_table, мы будем использовать:

CREATE OR REPLACE VIEW p_intersections AS    -- Create a view with the 
SELECT t1.the_geom as t1_geom,               -- intersecting geoms. Each pair
       t2.the_geom as t2_geom                -- appears once (t2.id<t2.id)
    FROM polygons_table t1, polygons_table t2  
         WHERE t1.id<t2.id AND t1.the_geom && t2.the_geom 
                           AND intersects t1.the_geom, t2.the_geom;

Теперь у нас есть представление (практически таблица только для чтения), в котором хранятся пары пересекающихся геом, где каждая пара появляется только один раз из-за t1.id<t2.idусловия.

Теперь давайте собирать ваши перекрестков - A∖AB, ABи B∖AB, используя SQL для UNIONвсех трех запросов:

--AB:
SELECT ST_intersection(t1.the_geom, t2.the_geom) 
    AS geom 
    FROM p_intersections

UNION 

--A∖AB:
SELECT ST_Difference(t1.the_geom, t2.the_geom) 
    AS geom 
    FROM p_intersections

UNION

--B∖AB:
SELECT ST_Difference(t2.the_geom, t1.the_geom) 
    AS geom 
    FROM p_intersections;

Заметки:

1. &&Оператор используется в качестве фильтра перед intersectsоператором, чтобы улучшить производительность.
2. Я решил создать VIEWвместо одного гигантского запроса; Это только для удобства.
3. Если вы имели в виду ABобъединение, а не пересечение, Aи B- используйте ST_Union вместо st_intersection при UNIONзапросе в соответствующих местах.
4. ∖Знак является юникода знак разности Set; удалите его из кода, если это смущает вашу базу данных.
5. Фотографии любезно предоставлены категорией теории множеств Викимедиа .

То, что вы описываете, - это способ работы оператора Union в ArcGIS, но он немного отличается от Union или Intersection в мире GEOS. В руководстве Shapely есть примеры того, как наборы работают в GEOS . Тем не менее, PostGIS Wiki имеет хороший пример использования linework, который должен помочь вам.

Кроме того, вы можете рассчитать три вещи:

1. ST_Intersection (geom_a, geom_b)
2. ST_Difference (geom_a, geom_b)
3. ST_Difference (geom_b, geom_a)

Это должны быть три полигона, которые вы упомянули во втором пункте.

Что-то типа:

INSERT INTO new_table VALUES ((выберите id, the_geom из old_table, где st_intersects (the_geom, (выберите the_geom из old_table, где id = '123')) = true

РЕДАКТИРОВАТЬ: вам нужно фактическое пересечение многоугольника.

INSERT INTO new_table значения ((выберите id, ST_Intersection (the_geom, (выберите the_geom из старого, где id = 123))

посмотрим, получится ли это.