Анализ операционного усилителя: когда применимы «правила отрицательной обратной связи»?

9

Когда мы создаем схемы ОУ, которые используют отрицательную обратную связь, вот так:

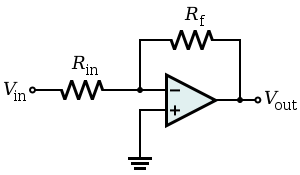
... мы можем очень легко проанализировать схему, предполагая, что из-за отрицательной обратной связи (конечно, когда предполагается, что операционный усилитель идеален).

v^{-} = v^{+}

$v^- = v^+$

Помимо очевидных случаев высокой точности, когда эти упрощенные модели ломаются, когда это и когда это не верно?
Например, если мы заменим резистор обратной связи каким-либо другим элементом - возможно, конденсатором, индуктором, диодом (обычный кремниевый диод, стабилитрон и т. Д.) Или какой-либо их комбинацией и другими элементами общей цепи - как мы узнаем, где это упрощение действительно?
Кроме того, даже если мы используем резистор в качестве элемента обратной связи, так как сопротивление становится очень, очень высоким, в какой-то момент мы можем в значительной степени считать его разомкнутой цепью, и, очевидно, эта модель ломается где-то по пути.

Итак, вопрос заключается в следующем: при каких ограничениях это приближение является «достаточно верным», чтобы дать полезные результаты?

РЕДАКТИРОВАТЬ:

Для другого примера рассмотрим базовую схему инвертирующего логарифмического усилителя:

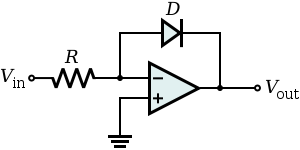
Если мы решим уравнение диода Шокли

i_{D} = I_{S} (e^{v D / V T} - 1)

$i_D = I_S(e^{vD/VT} - 1)$

для vD мы получаем (игнорируя 1, что в основном не имеет значения, поскольку экспонента будет довольно большой)

v_{D} = V T \ln (\frac{i_{D}}{I_{S}})

$v_D = VT \ln{\left(\frac{i_D}{I_S} \right)}$

Если затем мы используем виртуальный метод short, чтобы увидеть, что мы получим правильное выражение для вывода:

i_{D} = \frac{v_{i n} - 0}{R_{i n}}

$i_D = \frac{v_{in} - 0}{R_{in}}$

v_{o u t} = - V T \cdot \ln (\frac{v_{i n}}{I_{S} R_{i n}})

$v_{out} = -VT \cdot \ln{\left( \frac{v_{in}}{I_S R_{in}} \right)}$

Итак, виртуальный короткий метод работает здесь. Но так как этот диод будет разомкнутой цепью, когда я не уверен, как заранее выяснить, что анализ будет действительным.

v_{o u t} > v^{-}

$v_{out} > v^-$

— exscape
источник

С идеальной ОУ, то +и -терминалы будут равны независимо от использования ОУ в цепи.

— kevlar1818

2

@ kevlar1818 Как это будет работать? Если между выходом и входами нет связи, как это может изменить входы?

— exscape

Смотрите мой ответ для уточнения.

— kevlar1818

@ kevlar1818: Предположение о том, что входы операционного усилителя будут одинаковыми, зависит в некоторой степени не только от того, что операционный усилитель является идеальным, но и от других компонентов схемы. Если другие компоненты в цепи приводят к тому, что первая производная напряжения тракта обратной связи по отношению к выходному напряжению равна нулю (как могло бы случиться, если есть какая-либо некомпенсированная задержка RC), операционный усилитель не сможет мгновенно сбалансировать входные сигналы в ответ шаг стимула.

— суперкат

7

Как вы сказали, тот факт, что два входа усилителя будут почти одинаковыми, является упрощением и зависит от параметров, которые часто не указаны явно. Это хороший вопрос, так как важно знать пределы любых ярлыков или практических правил, которые вы используете.

Как уже говорил Клабаккио, одно из предположений, нарушающих допущение, заключается в том, что выход операционного усилителя обрезан или ему потребуется выходить за пределы доступного диапазона, чтобы получить желаемый сигнал. Другие причины, делающие предположение недействительным, включают:

Отзыв не отрицательный. Это может звучать глупо, но на самом деле я показал кому-то простую схему гистерезиса операционных усилителей в интервью и попросил их нарисовать график выходного напряжения как функции входного напряжения. Больше чем один кандидат начал, сказав, что операционный усилитель попытается сохранить свои два входа одинаковыми, а затем зарылся в более глубокую дыру оттуда. Излишне говорить, что это были короткие интервью.
Выгода не достаточна. Обратите внимание, что правило поддержания равных входов предполагает бесконечное усиление. Аналогично, правило, что Gain = -Rf / Rin предполагает бесконечное усиление. Обычно коэффициент усиления в разомкнутом контуре составляет около 100 тыс. Или более, и мы не просим более 100 или, может быть, не более 1000 за один этап, поэтому может показаться, что это небольшая проблема.

Однако это забывает о влиянии частоты на усиление. Операционный усилитель 1 МГц может быть указан для усиления по напряжению в разомкнутом контуре 100 кОм при постоянном токе, но если вы используете его для аудио и хотите пропускать 20 кГц, то коэффициент усиления в разомкнутом контуре в худшем случае будет только 50 Если вы установите резисторы обратной связи на усиление 25, это только оставит 2-кратный запас на верхнем уровне, что серьезно уменьшит усиление в замкнутом контуре на высоких частотах.
Ограничение скорости нарастания. Даже при достаточном усилении и правильной обратной связи, операционный усилитель может только так быстро менять свою мощность. Вот для чего нужна спецификация скорости нарастания. Коэффициент усиления * для полосы пропускания предназначен для малых сигналов. Сигналы большой амплитуды могут столкнуться с проблемами скорости нарастания. Для большинства операционных усилителей выходной сигнал полного размаха имеет более низкую частоту, чем то, что подразумевает произведение коэффициента усиления на полосу пропускания.

— Олин Латроп
источник

Хороший ответ. Я предположил, что операционный усилитель идеален, потому что в противном случае гипотезы всегда ложны :)

— clabacchio

4

До тех пор, пока операционный усилитель может устанавливать входы равными, управляя выходом при определенном напряжении, он будет.

Это предположение падает, когда это невозможно, например, если в обратной связи имеется разомкнутая цепь (положительная или отрицательная). Затем он будет насыщаться на одном из рельсов, в зависимости от того, какой вход повышен. Обратите внимание, что обратная связь разомкнутой цепи также может быть обратным диодом.

Другой случай может быть, если напряжение, которое позволяет равновесие на входах, превышает напряжения насыщения. Опять же, операционный усилитель будет насыщаться, а вход будет дисбалансирован.

Но почему входы должны быть равны?

Операционный усилитель имеет три рабочих области, одну из которых называют областью с высоким коэффициентом усиления , и две области насыщения . Правило о том, что входы должны быть одинаковыми, справедливо только для области с высоким коэффициентом усиления и вытекает из того факта, что для идеального операционного усилителя:

V_{o u t} = \infty (V_{d}) = \infty (V_{+} - V_{-})

$V_{out} = \infty (V_d) = \infty (V_+ - V_-)$

Это означает, что выходное напряжение является конечным только в том случае, если входные напряжения равны, поэтому операционный усилитель принудительно выставит выходное напряжение на значение, которое обнуляет разницу.

Когда операционный усилитель насыщается, выходное напряжение просто дается

V_{o u t} = V_{s a t}

$V_{out} = V_{sat}$

Это означает, что операционный усилитель делает все возможное, чтобы установить равные входы, но он сталкивается с подвижной стеной. Таким образом, входы могут разбалансироваться, чтобы удовлетворить выходное напряжение.

В вашем примере вы можете обнаружить, что операционный усилитель насыщается, когда входной сигнал равен или больше чем:

V_{i n}^{S A T -} = - V_{S A T -} \frac{R_{i n}}{R_{f}}

$V_{in}^{SAT-} = - V_{SAT-}\frac{R_{in}}{R_{f}}$

В вашем примере схемы, когда Vin отрицателен, V + будет выше, а затем выход будет насыщаться. Тогда обратная связь не сможет восстановить равновесие, потому что диод будет перевернут, поэтому для каждого отрицательного входа на выходе будет напряжение насыщения.

— клабаккио
источник

Спасибо, но я уже знал большую часть этого (я проанализировал тонны различных схем ОУ, но у них всех было одно общее: обычно было очевидно, будет ли этот метод применяться или нет). Я предполагаю, что меня смущает то, что считается разомкнутой цепью - например, диод может быть один (по крайней мере, идеальный), но метод, похоже, все еще работает там. Я добавил пример лог усилителя.

— exscape

Я просто помню тебя в те старые времена! Меня интересует формула насыщения (последняя. Не могли бы вы дать мне ссылку на эту формулу, а не просить вас больше поговорить об этом?

— hbak

2

В этом ответе я делаю вывод передаточной функции и делаю вывод, почему мы можем предположить, что оба входа равны.

Существует небольшое упрощение в расчете, которое простительно, если коэффициент усиления разомкнутого контура очень высок. Это верно для большинства операционных усилителей, я использовал цифру 100 000.

$\times$

— stevenvh
источник