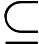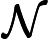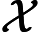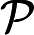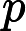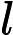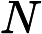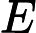Необоснованная сила неоднородности

С общей точки смысле зрения, легко поверить , что добавление индетерминизм к значительно расширяет свою власть, т.е. N P гораздо больше , чем P . В конце концов, недетерминизм допускает экспоненциальный параллелизм, который, несомненно, кажется очень мощным. $\mathsf{P}$$\mathsf{NP}$$\mathsf{P}$

С другой стороны, если мы просто добавить неравномерность в , получение P / р о л у , то интуиция менее ясна (предполагая , что мы исключаем нерекурсивные языков , которые могут возникнуть в Р / р о л у ). Можно ожидать, что простое использование разных алгоритмов полиномиального времени для разных входных длин (но не выход из рекурсивного царства) является менее мощным расширением, чем экспоненциальный параллелизм в недетерминизме.$\mathsf{P}$$\mathsf{P}/poly$$\mathsf{P}/poly$

Интересно, однако, что если мы сравним эти классы с очень большим классом , то увидим следующую нелогичную ситуацию. Мы знаем, что N E X P правильно содержит N P , что неудивительно. (В конце концов, N E X P допускает двукратно экспоненциальный параллелизм.) С другой стороны, в настоящее время мы не можем исключить N E X P ⊆ P / p o l y .$\mathsf{NEXP}$$\mathsf{NEXP}$ $\mathsf{NP}$$\mathsf{NEXP}$$\mathsf{NEXP}\subseteq \mathsf{P}/poly$

Таким образом, в этом смысле неравномерность при добавлении к полиномиальному времени, возможно, делает его чрезвычайно мощным, потенциально более мощным, чем недетерминизм. Это может даже пойти так далеко, что имитирует двоякий экспоненциальный параллелизм! Хотя мы считаем, что это не так, но тот факт, что в настоящее время это невозможно исключить, все же предполагает, что теоретики сложности борются здесь с «могущественными силами».

Как бы вы объяснили разумному дилетанту, что стоит за этой «необоснованной силой» неравномерности?

Отвратительный ответ: это не первая вещь в теории сложности, которую я бы попытался объяснить непрофессионалу! Чтобы даже оценить идею неоднородности и то, как она отличается от недетерминизма, вы должны быть в глубине сорняков с определениями классов сложности, чем многие люди хотят получить.

Сказав это, одна перспектива, которую я нашел полезной при объяснении P / poly студентам, заключается в том, что неравномерность действительно означает, что вы можете иметь бесконечную последовательность лучших и лучших алгоритмов, поскольку вы переходите к все большей и большей входной длине. На практике, например, мы знаем, что простой алгоритм умножения матриц лучше всего работает для матриц размером до 100x100 или около того, а затем в некоторый момент умножение Штрассена становится лучше, а затем более поздние алгоритмы становятся лучше только для астрономически больших матриц, которые никогда не возникнет на практике. Итак, что если бы у вас была магическая способность сосредоточиться на наилучшем алгоритме для любого диапазона n, с которым вы работали?

Конечно, это была бы странная способность, и, учитывая все обстоятельства, вероятно, не так полезна, как способность решать NP-полные задачи за полиномиальное время. Но, строго говоря, это была бы несравненная способность: вы не получите ее автоматически, даже если P = NP. В самом деле, вы даже можете построить надуманные примеры невычислимых задач (например, если в качестве входных данных 0 ⁿ останавливает ли n- ^ая машина Тьюринга?), Что эта способность позволит вам решить. Итак, это сила неоднородности.

Чтобы понять смысл рассмотрения этой странной силы, вам, вероятно, нужно что-то сказать о поиске, чтобы доказать нижние границы схемы, и тот факт, что с точки зрения многих из наших методов нижней границы, это единообразие, которое кажется странным дополнительные условия, которые нам почти никогда не нужны.

$O(2^{2n})$$O(2^{n})$$n$$(1+o(1))2^n/n$$\mathsf{SIZE}(f(n))$$\mathsf{DTIME}(f(n)^{O(1)})$$f(n)$$2^{O(n)}$

$\mathsf{NP} \subseteq \mathsf{P/poly}$

$\mathbb{P/poly}$$\mathbb{NP}$$\mathbb{P}$$\mathbb{NP}$

$\mathbb{P/poly}$$\mathbb{NP}$

$\mathbb{NP}$

$\mathbb{NP}$$\mathbb{P/poly}$

Критическим моментом для хорошего понимания, которое, как мне кажется, также является распространенным явлением при преподавании предмета в первый раз, является прояснение того, что совет и «подсказка» (то есть сертификат) - это разные вещи, и как они отличаются.

Для меня самой яркой иллюстрацией силы неоднородности является то, что подходяще дополненная версия проблемы остановки уже есть в P / 1. Тогда достаточно одного совета, чтобы выбрать этот язык с тривиальной ТМ, которая просто возвращает бит рекомендации.

Конечно, добавление неразрешимого языка в геометрической прогрессии означает, что в P / poly это не «морально». Но это показывает, что нужно быть осторожным, допуская неравномерность.

У меня сложилось впечатление, что реальная проблема здесь - неоправданно тяжелое бремя доказывания, а не необоснованная сила неоднородности. Как уже подчеркивалось в ответах Чазизопа и Андраса Саламона, неразрешимые языки становятся вычислимыми даже в очень ограниченных неоднородных языках, потому что бремя доказывания полностью снято.

$2^n$$n$$n$$n$$n$$2^n\exp(O(n))=\exp(n\log(2)+O(n))=\exp(O(n))$

$n$$\mathsf{NEXP}$

$\mathsf{P/poly'}\subseteq \mathsf{NP}$$n$$\mathsf{P/poly'}$$\mathsf{P}$$\mathsf{NP}\subseteq\mathsf{P/poly'}$) все еще верно, но это утверждение менее интересно, чем реальная теорема Карпа-Липтона.