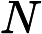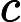Должны ли мы считать

Многие эксперты считают, что гипотеза верна, и используют ее в своих результатах. Меня беспокоит то, что сложность сильно зависит от гипотезы P ≠ N $\mathsf{P} \neq \mathsf{NP}$$\mathsf{P} \neq \mathsf{NP}$

Итак, мой вопрос:

Пока гипотеза не доказана, можно / нужно ли рассматривать ее как закон природы, как указано в цитате из Штрассена? Или мы должны рассматривать это как математическую гипотезу, которая может быть когда-нибудь доказана или опровергнута?$\mathsf{P}\neq\mathsf{NP}$

Quote:

«Доказательства в пользу гипотез Кука и Валианта настолько подавляющи, а последствия их неудач настолько гротескны, что их статус, возможно, можно сравнить с состоянием физических законов, а не с обычными математическими предположениями».

[ Приветствие Фолькера Штрассена лауреату Неванлиннской премии Лесли Г. Валиану в 1986 году]

Я задаю этот вопрос при чтении поста Физика результатов в TCS? , Возможно, интересно отметить, что вычислительная сложность имеет некоторые сходства с (теоретической) физикой: многие важные результаты сложности были доказаны при допущении , в то время как в теоретической физике результаты доказаны при допущении некоторых физических законов$\mathsf{P} \neq \mathsf{NP}$ . В этом смысле можно считать чем-то вроде E = m c 2 . Вернуться к физике результатов в TCS? :$\mathsf{P} \neq \mathsf{NP}$$E = mc^2$

Может ли (часть) TCS быть отраслью естественных наук?

Разъяснение:

(см. ответ Суреша ниже)

Можно ли сказать, что гипотеза в теории сложности так же фундаментальна, как и физические законы теоретической физики (как сказал Штрассен)?$\mathsf{P}\neq\mathsf{NP}$

Заявление Штрассена необходимо поместить в контекст. Это было обращение к аудитории математиков в 1986 году, когда многие математики не имели высокого мнения о теоретической информатике. Полное утверждение

Некоторым из вас может показаться, что обсуждаемые здесь теории опираются на слабые основания. Они не. Доказательства в пользу гипотез Кука и Валианта настолько ошеломительны, а последствия их неудач настолько гротескны, что их статус, возможно, можно сравнить с состоянием физических законов, а не с обычными математическими предположениями.

Я уверен, что Штрассен имел беседы с чистыми математиками, которые говорили что-то вроде

«Вы строите всю теорию сложности на карточном домике. Что если P = NP? Тогда все ваши теоремы будут бессмысленными. Почему бы вам просто не приложить немного усилий и доказать, что P NP, а не продолжайте строить теорию на таких слабых основаниях ".$\neq$

В 2013 году, когда P NP был проблемой с призом Клея в течение десятка лет, может показаться трудным поверить, что у любого математика действительно были такие взгляды; однако, я могу лично подтвердить, что некоторые сделали.$\neq$

Штрассен продолжает, говоря, что мы не должны отказываться от поиска доказательства P NP (таким образом, косвенно подразумевая, что это действительно математическая гипотеза):$\neq$

Тем не менее, традиционные доказательства представляют большой интерес, и мне кажется, что гипотеза Валианта может быть легче подтвердить, чем гипотеза Кука ...

так что, возможно, я бы назвал это «рабочей гипотезой», а не «физическим законом».

Позвольте мне наконец отметить, что математики также используют такие рабочие гипотезы. Существует большое количество математических работ, доказывающих теоремы, утверждения которых гласят: «Если предположить, что гипотеза Римана верна, то ...».

Я вижу три взаимосвязанных способа понять вопрос:

1) Можем ли мы считать фундаментальным принципом теории сложности вычислений еще до того, как мы сможем это доказать?$NP \ne P$

2) Распространяется ли принцип за пределы своего узкого математического значения?$NP \ne P$

3) Можно ли рассматривать принцип как физический закон?$NP \ne P$

Я думаю, что есть веские причины для ответа «да» или «квалифицировано да» на все эти три вопроса.

Я не уверен, что понимаю. Физический закон (того типа, который вы указываете) - это математическое выражение модели (в этом примере, относительности), которая претендует на захват реальности. Физический закон может быть доказан неверным, если базовая математика неверна, но он также может быть неправильным, если базовая модель изменяется (например, ньютоновская механика). P против NP - это конкретная математическая гипотеза, которая является истинной или ложной (и может быть доказуемо или нет)

Чтобы ответить на ваш оригинальный вопрос:

$P \ne NP$

«Допущение твердости NP ?: Нет физических средств для решения полных задач NP за полиномиальное время».

Он выступил с хорошей речью в Университете Ватерлоо под названием « Вычислительная неразрешимость как закон физики».

$NL\neq PSPACE$$NP\neq coNP$$P\neq NP$

$\phi$$\phi$

Вы можете провести множество экспериментов на скоростях и скоростях, и вы получите неопровержимые доказательства, подтверждающие законы Ньютона. Конечно, вы увидите некоторые очень странные вещи в очень специфических экспериментах, такие как скорость света в движущейся воде или некоторые астрономические события. Но ваши убедительные доказательства скажут вам: Ньютон прав, и эти законы - то, что вам нужно.

Конечно, Ньютон «не прав», и Эйнштейн последовал за ним.

Для P = NP мы можем видеть множество примеров, где кажется, что P ≠ NP. Но в некоторых частных случаях у нас есть странные вещи. Если P ≠ NP, существует бесконечное число классов между ними, поэтому мы должны найти некоторые проблемы в NP, которые не находятся в P, но не являются NP-полными. Мы не знаем ни одного из них, и большинство кандидатов оказались в P.

Что вы думаете об этой проблеме, зависит от того, куда вы хотите посмотреть. Я не удивлюсь, если P = NP.