Проблема может быть решена в O (polylog (b)).
Мы определяем f(d, n)число целых чисел до d десятичных цифр с суммой цифр, меньшей или равной n. Видно, что эта функция задается формулой

Давайте выведем эту функцию, начиная с чего-то более простого.
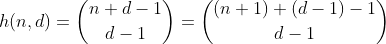
Функция h считает количество способов выбора d - 1 элементов из множества, содержащего n + 1 различных элементов. Это также количество способов разбить n на d бинов, что легко увидеть, построив d - 1 заборы вокруг n и суммируя каждый отдельный раздел. Пример для n = 2, d = 3 ':
3-choose-2 fences number
-----------------------------------
11 ||11 002
12 |1|1 011
13 |11| 020
22 1||1 101
23 1|1| 110
33 11|| 200
Таким образом, h считает все числа, имеющие цифру-сумму из n и d цифр. За исключением того, что он работает только для n менее 10, так как цифры ограничены 0 - 9. Чтобы исправить это для значений 10 - 19, нам нужно вычесть количество разделов, имеющих один бин с числом больше 9, которое теперь я буду называть переполненными бинами.
Этот термин может быть вычислен путем повторного использования h следующим образом. Мы подсчитываем количество способов разбиения n - 10, а затем выбираем один из бинов, в который нужно поместить 10, в результате чего количество разделов имеет один переполненный бин. Результатом является следующая предварительная функция.
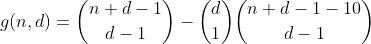
Мы продолжаем этот путь для n, меньшего или равного 29, подсчитывая все способы разбиения n - 20, затем выбирая 2 ячейки, в которые мы помещаем десятки, таким образом подсчитывая количество разделов, содержащих 2 переполненных ячейки.
Но в этот момент мы должны быть осторожны, потому что мы уже посчитали разделы, имеющие 2 переполненных бина в предыдущем семестре. Не только это, но на самом деле мы насчитали их дважды. Давайте рассмотрим пример и рассмотрим разбиение (10,0,11) с суммой 21. В предыдущем семестре мы вычли 10, вычислили все разделы из оставшихся 11 и поместили 10 в один из 3 лотков. Но этот конкретный раздел может быть достигнут одним из двух способов:
(10, 0, 1) => (10, 0, 11)
(0, 0, 11) => (10, 0, 11)
Поскольку мы также посчитали эти разделы один раз в первом члене, общее количество разделов с 2 переполненными ячейками составляет 1 - 2 = -1, поэтому нам нужно подсчитать их еще раз, добавив следующий член.
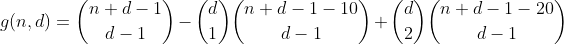
Подумав об этом немного подробнее, мы вскоре обнаружим, что число раз, которое раздел с определенным количеством переполненных бинов подсчитывается в определенном термине, может быть выражено следующей таблицей (столбец i представляет термин i, строка j разделов с j переполнением бункера).
1 0 0 0 0 0 . .
1 1 0 0 0 0 . .
1 2 1 0 0 0 . .
1 4 6 4 1 0 . .
. . . . . .
. . . . . .
Да, это треугольник Паскаля. Единственный интересующий нас счет - это число в первой строке / столбце, то есть количество разделов с нулевыми переполненными ячейками. А так как переменная сумма каждой строки, кроме первой, равна 0 (например, 1 - 4 + 6 - 4 + 1 = 0), мы избавляемся от них и получаем предпоследнюю формулу.
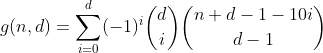
Эта функция считает все числа с d цифрами, имеющими сумму цифр n.
А как насчет чисел с цифрой-суммой меньше n? Мы можем использовать стандартное повторение для биномов плюс индуктивный аргумент, чтобы показать, что
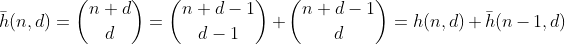
подсчитывает количество разделов с цифрой-суммой не более n. И из этого f можно получить, используя те же аргументы, что и для g.
Используя эту формулу, мы можем, например, найти число тяжелых чисел в интервале от 8000 до 8999, поскольку 1000 - f(3, 20), поскольку в этом интервале есть тысячи чисел, мы должны вычесть число чисел с суммой цифр, меньшей или равной 28 принимая во внимание, что первая цифра уже вносит 8 в сумму цифр.
В качестве более сложного примера давайте посмотрим на число тяжелых чисел в интервале 1234..5678. Сначала мы можем перейти с 1234 до 1240 с шагом 1. Затем мы с 1240 до 1300 с шагом 10. Приведенная выше формула дает нам число тяжелых чисел в каждом таком интервале:
1240..1249: 10 - f(1, 28 - (1+2+4))
1250..1259: 10 - f(1, 28 - (1+2+5))
1260..1269: 10 - f(1, 28 - (1+2+6))
1270..1279: 10 - f(1, 28 - (1+2+7))
1280..1289: 10 - f(1, 28 - (1+2+8))
1290..1299: 10 - f(1, 28 - (1+2+9))
Теперь мы идем от 1300 до 2000 с шагом 100:
1300..1399: 100 - f(2, 28 - (1+3))
1400..1499: 100 - f(2, 28 - (1+4))
1500..1599: 100 - f(2, 28 - (1+5))
1600..1699: 100 - f(2, 28 - (1+6))
1700..1799: 100 - f(2, 28 - (1+7))
1800..1899: 100 - f(2, 28 - (1+8))
1900..1999: 100 - f(2, 28 - (1+9))
От 2000 до 5000 с шагом 1000:
2000..2999: 1000 - f(3, 28 - 2)
3000..3999: 1000 - f(3, 28 - 3)
4000..4999: 1000 - f(3, 28 - 4)
Теперь нам нужно снова уменьшить размер шага: с 5000 до 5600 с шагом 100, с 5600 до 5670 с шагом 10 и, наконец, с 5670 до 5678 с шагом 1.
Пример реализации Python (который получил небольшую оптимизацию и тестирование):
def binomial(n, k):
if k < 0 or k > n:
return 0
result = 1
for i in range(k):
result *= n - i
result //= i + 1
return result
binomial_lut = [
[1],
[1, -1],
[1, -2, 1],
[1, -3, 3, -1],
[1, -4, 6, -4, 1],
[1, -5, 10, -10, 5, -1],
[1, -6, 15, -20, 15, -6, 1],
[1, -7, 21, -35, 35, -21, 7, -1],
[1, -8, 28, -56, 70, -56, 28, -8, 1],
[1, -9, 36, -84, 126, -126, 84, -36, 9, -1]]
def f(d, n):
return sum(binomial_lut[d][i] * binomial(n + d - 10*i, d)
for i in range(d + 1))
def digits(i):
d = map(int, str(i))
d.reverse()
return d
def heavy(a, b):
b += 1
a_digits = digits(a)
b_digits = digits(b)
a_digits = a_digits + [0] * (len(b_digits) - len(a_digits))
max_digits = next(i for i in range(len(a_digits) - 1, -1, -1)
if a_digits[i] != b_digits[i])
a_digits = digits(a)
count = 0
digit = 0
while digit < max_digits:
while a_digits[digit] == 0:
digit += 1
inc = 10 ** digit
for i in range(10 - a_digits[digit]):
if a + inc > b:
break
count += inc - f(digit, 7 * len(a_digits) - sum(a_digits))
a += inc
a_digits = digits(a)
while a < b:
while digit and a_digits[digit] == b_digits[digit]:
digit -= 1
inc = 10 ** digit
for i in range(b_digits[digit] - a_digits[digit]):
count += inc - f(digit, 7 * len(a_digits) - sum(a_digits))
a += inc
a_digits = digits(a)
return count
Редактировать : заменен код на оптимизированную версию (которая выглядит даже хуже, чем исходный код). Также исправил несколько угловых случаев, пока я был на нем. heavy(1234, 100000000)занимает около миллисекунды на моей машине.
