Если бы вы жили на противоположной стороне Луны, как вы могли бы сделать вывод о существовании Земли?

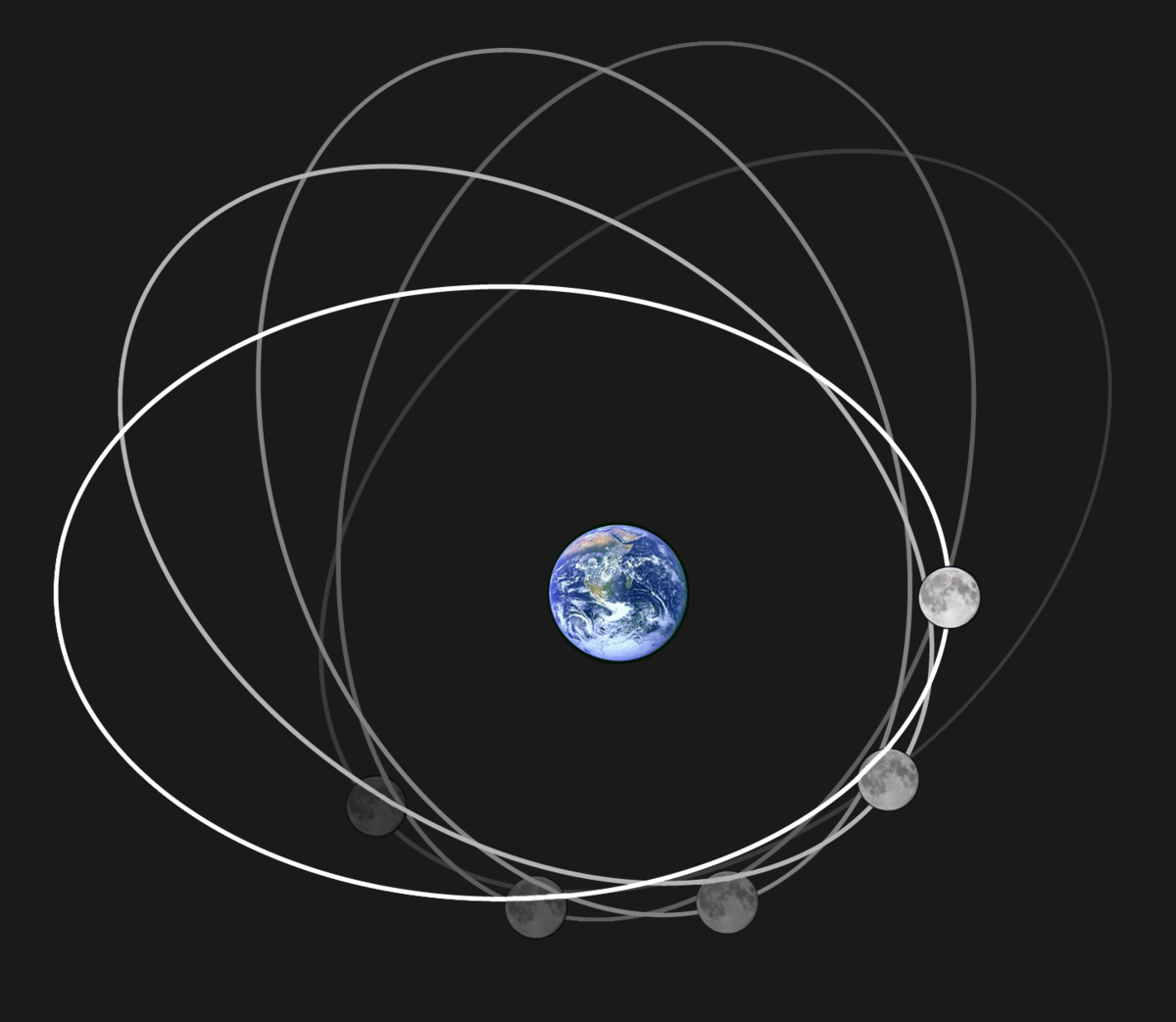
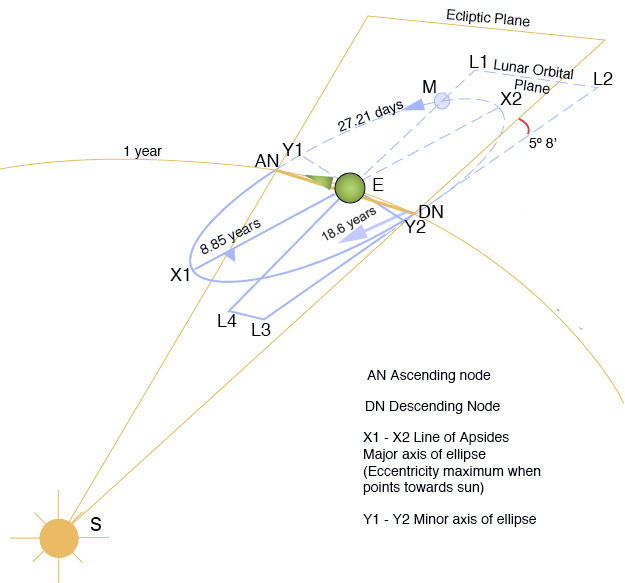
Предположим, что вы положили астронома, вооруженного нашими современными знаниями об орбитальной механике, на купол на противоположной стороне Луны, чтобы Земля постоянно скрывалась от них.

(И, конечно, предположим, что у этого человека нет конкретных знаний о системе, в которой он находится, помимо того, что он может почерпнуть из наблюдений. Если хотите, представьте, что он изучил всю нашу современную орбитальную механику и связанную с ней физику в альфа-центавриане, и затем телепортировался на нашу Луну.)

Теперь разумно ожидать, что этот человек должен быть в состоянии вывести из наблюдений неба, что тело, на котором он находится, является половиной двойной системы, и он должен быть в состоянии измерить орбитальные характеристики (большая полуось, эллиптичность, наклон), а также положение барицентра (гораздо ближе к другому телу, что соответствует гораздо более массивному партнеру). Какие наблюдения необходимы, чтобы сделать это? Какой уровень точности наблюдений необходим для этих наблюдений и какой исторической эпохе он соответствует? (То есть было бы достаточно набора Тихо Браге? Будет ли набор Галилея? Будет ли у древних греков? Или для этого потребуется обсерватория конца 19-го века (или даже позже)?)

(Как указано в ответе MartinV, нашему астроному может быть трудно различить ситуации с орбитальной парой и одним огромным телом. Таким образом, если это удобно, можно предположить, что через короткие ~ 100 км вылеты от купола наш астроном способный измерять лунный радиус, измеряя солнечные наклоны в различных точках с известными расстояниями между ними, как Erathostenes .)

— Эмилио Пизанти
источник

Звездный параллакс окончательно помог бы, и это 19 век.

@ LucJ.Bourhis Звездный параллакс, или, по крайней мере, его ведущий компонент, идет с радиусом орбиты вокруг Солнца, и компоненты лунной орбиты будут намного меньше, чем это, так что это выглядит как неочевидное решение для меня (и это не очевидно, что наблюдения 19-го века также обеспечат необходимую точность). Я подозреваю, что наиболее вероятным кандидатом является параллакс Солнца относительно звездного фона (или, что эквивалентно, положения звезд относительно часов, синхронизированных с лунным днем), но я хотел бы знать, с какой точностью (по сравнению с историческими ссылками) вы ' мне нужно для этого.

— Эмилио Пизанти

Конечно! Это не то, что я имел в виду. Исторически тот факт, что Луну можно наблюдать с Земли, сыграл важную роль в измерении расстояния Земля-Солнце, от которого многое зависит. Я думал об использовании параллакса, чтобы справиться с этим расстоянием.

Тем не менее, полмесячный параллакс может быть полезен для чего-то вроде Марса. Диаметр орбиты Луны составляет ~ 0,0026 а.е., Марс может быть на расстоянии ~ 1 а.е., так что угол составляет ~ 0,0052 радиана или 0,3 градуса, нет? Не уверен, как они сравниваются с наблюдениями звездного параллакса на протяжении многих лет, но кажется, что это может сместить положение Марса относительно отдаленных звезд в видимой форме.

Интересно, было бы достаточно 5-градусного наклона Луны. (5,14 градуса), что составляет примерно 9% от его орбитального расстояния вверх и вниз каждые 29 дней) или 1/6 от 1 градуса относительно Солнца. Относительно Марса на близком проходе, немного меньше. 14 дней наблюдения за тем, как Марс движется вверх или вниз, но не согласованно, так как, иногда вверх, иногда вниз, может быть наиболее заметным.

— userLTK

Ответы:

Тело прилив Сейсмометр на дальней стороне Луны будет забрать как солнечный прилив, и 20 дюймов тела искажения производимого земли . В то время как «приливно-откидной» замок, Луна не находится на идеально круговой орбите, а также немного колеблется; либрации . Ваш сейсмометр должен уловить оба эффекта.

Наблюдение за циклом параллакса Марса каждые 28 дней, как предлагается в комментариях выше, может быть более простым способом.

— странствующий незнакомец
источник

Это интересный ответ. Земля действительно поднимет небольшой «прилив» на Луну, и либрация заставит ее двигаться. Эффект небольшой и тонкий - сам по себе, позволит ли он умному ученому сделать вывод о существовании неизвестного и невидимого тела в космосе?

— MartinV

Сейсмические эффекты интересны, хотя мне непонятно, как их можно измерить. И да, я согласен, что параллакс является наиболее вероятным ответом, но я искал что-то более количественное и подробное.

— Эмилио Пизанти

Это действительно хороший вопрос - и довольно тонкий.

TL; DR;

Самая ранняя возможность может состоять в том, что межмесячные изменения в звёздном параллаксе Солнца могут привести наблюдателя к выводу, что либо i) Луна - это одно очень большое вращающееся тело, либо ii) она является частью многочастичного спутника. вращающаяся система. Однако я), казалось бы, несовместимо с близким и сильно изогнутым горизонтом.

Если нет, то, конечно, когда мы разработаем количественную модель орбитальной механики, включающей массу и гравитацию

Я не думаю, что звездный параллакс напрямую помог бы нам, поскольку он (в наши дни) просто говорит нам, что мы находимся на орбите вокруг Солнца и мало о самой системе Земля-Луна.

Давайте посмотрим, как это может увидеть эквивалент Птолемея на Луне (назовите его Луна-Птолемей). Он не мог бы отличить систему Земля-Луна от своего предположения о том, что он просто сидит на твердом объекте в центре творения. Конечно, он не увидит "луну" на орбите вокруг него, но он увидит Солнце, звезды и главные планеты. Звездный параллакс (для него Солнце, «движущееся через Зодиак») просто скажет ему, что Солнце вращается вокруг своей Луны, как и планеты. Существование планетарных эпициклов было бы любопытством, необходимым для того, чтобы его модель работала - но это делает работать, и он понятия не имеет о Земле

Луна-Галилей может (или не может) разработать гелиоцентрическую модель - он упускает одно ключевое понимание, которое было у Земли-Галилея: что Земля не была особенной, потому что на других планетах также были спутники. Луна-Галилео посчитал бы интересной орбитальную систему Юпитера, но не ключевой идеей, поэтому он может не разработать новую модель. Даже так, кто-то еще будет.

Тем не менее, в качественном научном мире все равно ничто не поможет наблюдателю Луны сделать вывод о существовании Земли за горизонтом.

Я подозреваю, что истина станет неизбежной, когда орбитальная механика разовьется достаточно, чтобы включить в расчет массу и гравитацию. Это могло быть во времена Луны-Кеплера.

Я не уверен, что согласен с комментариями, касающимися наблюдений за планетами - я не понимаю, как они помогают различать систему Земля-Луна в отличие от простого, очень большого, вращающегося тела Луны без спутника ( что было бы естественным предположением, чтобы сделать). Даже ежемесячные изменения параллакса, вызванные вращением Луны вокруг Земли, можно было бы отмахнуться, предложив простое вращение гораздо большего тела Луны - хотя наш герой, несомненно, может поставить под сомнение совместимость этого с очевидной кривизной и расстоянием до их Лунный горизонт.

— MartinV
источник

Кажется, я неправильно объяснил цель вопроса. Вы можете использовать современные знания орбитальной механики, если это необходимо ─ при проведении исторических сравнений, меня больше всего интересует экспериментальная техника, а не концептуальные достижения. Если хотите, вы можете думать о ситуации как об астрономе, который изучил всю современную орбитальную механику на альфа-центавриане, а затем телепортировался на поверхность нашей Луны. Итак, у них есть полное знание о том, как работают гравитация и механика, они просто не имеют никаких предварительных знаний о конкретной системе, в которой они находятся.

— Эмилио Пизанти

Но что касается вашего Луны-Птолемея, разве ему не нужно включать эпицикл для Солнца? Это наблюдение звездного параллакса, которое будет переведено в орбитальный радиус Земля-Луна, если вы переключитесь на гелиоцентрическую перспективу. Но насколько это было бы важно и насколько сложно это было бы измерить?

— Эмилио Пизанти

Спасибо Эмилио - на солнечном эпицикле, я думаю, что он, вероятно, будет слишком мал, учитывая оборудование, доступное Луне-Птолемею. На ваш другой комментарий - никаких недоразумений вообще; это был твой вопрос, так что я думаю, что я неправильно понял! Учитывая, что эксперт с современным оборудованием пересажен на Луну, я думаю, что они выяснят это довольно быстро - комбинация колебаний в параллаксе в сочетании с видимым размером Луны, несомненно, поставит вопрос. На самом деле, эксперт смотрел на саму маленькую каменистую Луну и сразу же задавал вопрос "что это за орбита?"

— MartinV

Да, я ожидаю, что они выяснят это довольно быстро; вопрос в том, как и какое оборудование им понадобится. (В вашем последнем предложении я не думаю, что это было бы естественным предварительным ожиданием, учитывая, как мало мы знаем о распространенности скалистых экзопланет. Но если взглянуть на поверхность просто, различия между Луной и Церерой минимальны Таким образом, поверхность не обязательно предполагает, что вы находитесь на спутнике. Вместо этого, учитывая радиус и гравитацию поверхности, скалистая поверхность и отсутствие атмосферы могут быть вполне естественными особенностями.)

— Эмилио Пизанти

Наблюдателю на противоположной стороне луны будет трудно объяснить, что он стоит на одной планете из-за движения самой заметной вещи на небе: солнца!

Действительно, из-за эксцентриситета орбиты Луны вокруг Земли, продолжительность дня, то есть «скорость солнца в небе», зависит от того, где вы находитесь на своей лунной орбите.

И из наблюдений, которые он может сделать, например, другие планеты, которые почти идеально круглые в Солнечной системе (и по хорошо известным причинам), она должна быть вынуждена исключить гипотезу «Я стою на эллиптическом одном небесном теле».

Я не могу рассчитать изменение продолжительности дня на дальней стороне Луны за разумное время, извините за это.

Еще один эффект, который я попытаюсь проиллюстрировать с помощью изображений из Википедии: высота солнечной траектории в небе будет меняться год за годом (цикл: от 8 до 9 земных лет) из-за апсидальной прецессии Луны и ее наклонного плана орбиты:

По Rfassbind - собственная работа., Public Domain, ссылка

Геолог, Гомункулус 2 - из английской Википедии, CC BY 3.0 , ссылка

— Дж. Чомел
источник